[leetcode 315]Count of Smaller Numbers After Self 原创解法

题目概述

原题链接

You are given an integer array nums and you
have to return a new counts array. 
The counts array has the property where counts[i] is 
the number of smaller elements to the right of nums[i].

Example:

Given nums = [5, 2, 6, 1]

To the right of 5 there are 2 smaller elements (2 and 1).
To the right of 2 there is only 1 smaller element (1).
To the right of 6 there is 1 smaller element (1).
To the right of 1 there is 0 smaller element.
Return the array [2, 1, 1, 0].

拿到这个题，最先想到的是时间复杂度O(N*N) 的解法。那就实现一下吧。

class Solution2(object):
    def countSmaller(self, nums):
        """
        O(N*N)
        :type nums: List[int]
        :rtype: List[int]
        """
        if nums:
            n = len(nums)
            result = []
            for i in range(n):
                cur_val = nums[i]
                smaller_n = 0
                for j in range(i, n):
                    if nums[j] < cur_val:
                        smaller_n += 1

                result.append(smaller_n)
            return result
        else:
            return []

把上面的代码提交上去，还是正确的，但是超时了。 该怎么优化呢？

遇到这样的问题，如果能够想出S(N)=f(S(N-1),S(N-2),...)这样的动态规划 解法 就可以把时间复杂度降到O(N)了。能不能使用动态规划呢？ 还是要仔仔细细列出来，可是怎么也找不到递推规律。只好放弃。不过在思考 的过程中忽然想到一种思路。对于数组[5, 2, 6, 1]]，如果我先遍历 求出5的smaller数组[2,1]和larger数组[6]。那么6的smaller个数怎么 求呢，s(6) = len([5,2,6,1]) - pos(6) = 4-3 = 1。看起来很不错，但是当 数的个数多起来，就变得复杂了，无法这样简单的求解了。真是非常的泄气啊。 想了好久也没有想出新点子。脑子里把曾经用到的方法想了一个遍， 也还是不行。

用二维图描述问题

物理学科中经常使用的一个策略就是转换坐标系，这样可以神奇的 化繁为简。那么我是否可以这样做呢。看看能不能用二维的图来重新展示这个问题。 于是我就画了这样一个图表。这是对数组[5,1,6,7,2,3]画的表格。横轴表示数组的index， 纵轴表示大小。

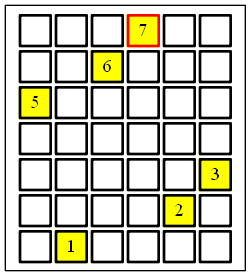
我把它画在纸上，盯着看了半小时。呵呵，真的有这么长时间。 因为我一直还是老思路，总想着根据第一个数字把剩下的数组分成大小两批。 后来我想，既然是二维图，我既可以从左向右，一列一列的看，也可以从上往下一行一行的 看。 不错，终于有了新的思路。

0. 初始化一个长度为N的smaller数组，用于存放最后的解。
1. 对原始数组从大到小排序。
2. 取出最大的数，这个数的 value = smaller_num(Nmax) = 数组的长度 - pos(Nmax)
3. 保存结果smaller[index(Nmax)] = value
4. 对于index大于该数的所有数字的index减一。
5. 重复2

如下图。首先找到最大的数字7，它的索引是4(第四个数字)， 而数组的长度为6，那么smaller_num("7") = 6 - 4 = 2。然后不考虑该数字7。 对7右侧的2和3同时向左移动，同时令数组的长度减一。然后依次这样操作。

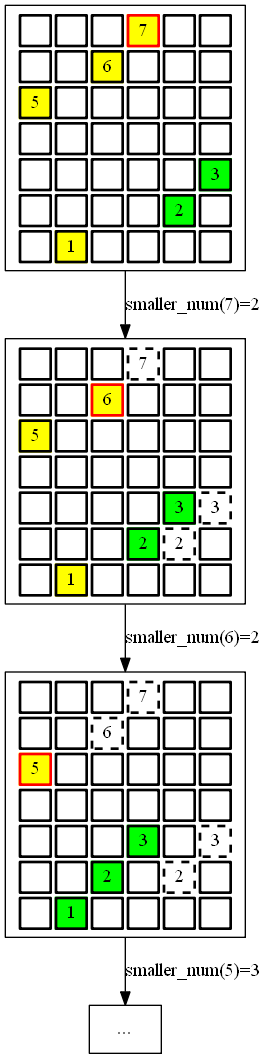
这样我们就可以写出一个新的算法。而对于步骤5则 使用了简单实现，遍历整个数组，对所有index > index(Nmax)数的索引进行 减一。上述算法描述没有考虑有多个最大值的情况。但是下面的代码里考虑了。

class Solution1(object):
    def countSmaller(self, nums):
        """
        O(N*N)
        :type nums: List[int]
        :rtype: List[int]
        """
        origin = list(enumerate(nums))
        l = self.create(nums)
        l.sort(cmp=compare, reverse=True)
        smaller = [0] * len(nums)
        i = 0
        N = len(nums)
        while i < len(l):
            v, origin_pos, cur_pos = l[i]
            smaller[origin_pos] = N - 1 - cur_pos
            equal_n = 0
            for j in range(i + 1, len(nums)):
                v1, origin_pos2, cur_pos2 = l[j]
                if cur_pos2 > cur_pos:
                    l[j][2] = cur_pos2 - 1
                    if v1 == v:
                        # 考虑值相等的情况。
                        equal_n += 1

            smaller[origin_pos] -= equal_n

            N -= 1
            i += 1

        return smaller

    def create(self, nums):
        result = []
        for i in range(len(nums)):
            result.append([nums[i], i, i])
        return result

终于通过了

事情终于有了进展，看起来很不错。但是仍然 遇到了时间复杂度过高的问题。因为实现步骤5的方法导致整个程序的 时间复杂度是O(N*N)。那么有什么办法能够优化呢。嗯，肯定有办法的。 我们这样来做。

1. 保存一个原始索引的(origin_index,value)的originList。
2. 再保存一个从大到小排序后的(origin_index,value)的lList。
3. 对l根据value从大到小进行遍历：根据orgin_index使用二分查找 查找origin中对应的实际索引，计算得到该值对应的smaller_num之后， 从origin中删除该项。

因为二分查找和删除项的时间复杂度是O(logN)。 上述步骤的总的时间复杂度是O(N*logN)。

而相等的数怎么办呢？嗯我们可以在排序 的时候保证序列不但满足值的升序，还能保证索引值的升序。 这样，原始数组中处于最右侧的最大数永远在序列的末尾。这个数的右侧不会有相等的值。 因而计算的时候就不需要考虑相等值的情况。 而该数字计算之后会进行删除。那么即使有相等的数，也不会受到影响。 真是很不错啊。

class Solution11(object):
    def countSmaller(self, nums):
        """
        O(NlogN)
        :type nums: List[int]
        :rtype: List[int]
        """
        origin = list(enumerate(nums))
        l = self.create(nums)
        l.sort(cmp=self.compare)
        smaller = [0] * len(nums)
        while l:
            v, pos = l.pop()
            cur_pos = self.bin_find(origin, pos)
            smaller[pos] = len(origin) - 1 - cur_pos
            origin.pop(cur_pos)

        return smaller

    def compare(self, x, y):
        # 这样排序那么相等的元素的仍然顺序不变
        if x[0] > y[0]:
            return 1
        elif x[0] == y[0]:
            return 1
        else:
            return -1

    def create(self, nums):
        result = []
        for i in range(len(nums)):
            result.append([nums[i], i])
        return result

    def bin_find(self, origin, pos):
        # 二分查找法
        start = 0
        end = len(origin)
        mid = (start + end) // 2
        new_mid = None
        while mid < len(origin) and mid >= 0:

            if origin[mid][0] == pos:
                break
            elif origin[mid][0] > pos:
                end = mid
                new_mid = (start + end) // 2
            elif origin[mid][0] < pos:
                start = mid
                new_mid = (start + end) // 2

            if new_mid == mid:
                mid += 1
            else:
                mid = new_mid

        return mid

总结

以上的解法是首先排序，再进行巧妙处理的一种方法。排序的 时间复杂度是O(N*logN)，接下来的处理也是O(N*logN)。